ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

Introduction

L’histoire des sciences est jalonnée de découvertes essentielles qui ont modifié le savoir des hommes, leur vision du monde, ou tout simplement leur vie quotidienne. A chacune de ces découvertes est lié un personnage auquel ses admirateurs, la rumeur populaire ont associé une phrase, une fable transformant le découvreur en héros mythique. La mémoire collective perpétue ainsi les légendes édifiantes de Newton et de sa pomme, de Galilée et de «et pourtant elle tourne», de Pasteur et du petit Joseph Meister; on assiste plus près de nous à la transformation en héros scientifiques de Marie Curie dans son laboratoire miteux et d’ Albert Einstein immortalisé autant par son poster que par sa formule (dont le sens est plus que relatif pour beaucoup).

Buste (imaginaire) d'Archimède - Musée National de Naples

Un des premiers savants légendaires est sans doute Archimède indissociable de sa baignoire et d’euréka. Son appartenance à la Grande Grèce a sans doute favorisé sa semi-déification et contribué à l’élaboration de sa légende. Ses admirateurs parmi lesquels Cicéron qui découvrit sa tombe, Plutarque, Léonard de Vinci, et plus tard Auguste Comte ont perpétué, enrichi les contes et légendes d’Archimède.

Vis d'Archimède (cochlea) - gravure du XVIIIe siècle (abbé Nollet)

Les certitudes concernant sa vie

• Archimède a vécu à Syracuse, opulente cité de Sicile qui faisait partie de la grande Grèce.
• C’était un ami du roi Hiéron.
• Il est mort âgé de 75 ans au cours du siège de Syracuse sous les coups d’un soldat romain.
• C’était un savant semblable à ceux qui ont pu exister jusqu’au XVIII ème siècle, c’est dire à la fois physicien, mathématicien, ingénieur et philosophe. En mathématiques, il perfectionna le système de numération des Grecs, permettant d'exprimer un nombre aussi grand que l'on veut. Il développa la géométrie d'Euclide (volumes de la sphère, du cylindre; coniques, spirales,...). Il donna un procédé pour calculer PI avec autant de précision que l'on veut. Il procéda à de véritables intégrations. Dans le domaine pratique, il imagina, entre autres, la vis sans fin qui porte son nom.
• Il a écrit plusieurs ouvrages, douze nous sont parvenus, on suppose que trois ou quatre ont été perdus. Il a écrit le premier traité scientifique de statique avec le principe du levier et les bases de l'hydrostatique qui porte son nom.

Les suppositions

• On ignore tout ce qui concerne sa vie personnelle, même la date de sa naissance (qu’on peut cependant calculer par différence: 287 av.JC); en effet, sa biographie, attribuée à Héraclite, a disparu.
• Tous les « portraits » le représentant sous les traits d’un vieillard barbu ou sous ceux d’un homme plus jeune courant dans les rues dans le plus simple appareil datent au mieux du XVème siècle.
• Il est possible qu’il ait effectué un voyage à Alexandrie, ville grecque d’Egypte, capitale intellectuelle, siège d’une immense bibliothèque. Sinon il a pu avoir une correspondance avec des savants résidant dans cette ville (Euclide fut sans doute un de ses maîtres).
• Les circonstances exactes de sa mort restent assez floues, Plutarque en donne trois versions plus ou moins édifiantes.

Les recherches et les découvertes d’Archimède en mathématiques et en physique ont été à l’origine d’autres études, et quelques unes sont au programme de nos lycées et collèges comme par exemple la mesure du volume par déplacement d’eau qui correspond au plus célèbre conte concernant Archimède.

ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

De la légende à la physique à l'école:

La couronne, le roi et le faussaire.

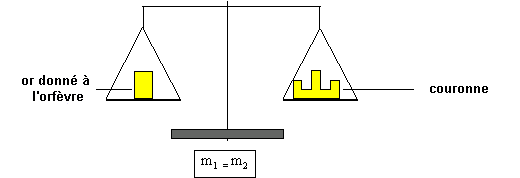
Un beau jour, le roi commanda une couronne en or pour l’offrir aux dieux, il donna à l’orfèvre la masse d’or nécessaire à la fabrication. La couronne réalisée était superbe, elle fut pesée, sa masse était identique à celle de l’or donné.

Pourtant le roi avait un doute la couronne ne semblait pas faite d’or pur. Il demanda à son ami Archimède de s’en assurer mais sans détruire l’ouvrage donc sans le fondre ni le scier.
Archimède chercha, chercha mais la notion de volume et à qui plus est la mesure du volume d’un solide de forme complexe ne faisait pas partie des connaissances scientifiques de l’époque.
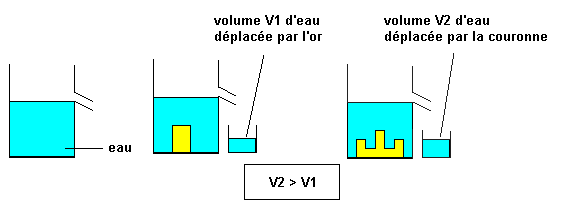
Comme ses contemporains Archimède était amateur de bains, en se plongeant dans une baignoire pleine il constata que celle-ci débordait et... Eurê Eurêka!, il avait trouvé: le problème était résolu. Il sauta hors de son bain, courut tout nu dans les rues pour annoncer sa découverte, il allait pouvoir mesurer le volume de la couronne et celui de l’or donné par déplacement d’eau.

La couronne avait un volume supérieur à celui de l’or donné, elle contenait donc un autre métal en l’occurrence de l’argent, qui pour un même volume a une masse plus faible que l’or.
La notion de masse volumique entrait dans l’histoire.
On dit maintenant que 1 m³ d’or a une masse de 19300 kg et que 1 m³ d’argent a une masse de 10500 kg.
Le roi s’était bel et bien fait avoir, l’orfèvre avait gardé une partie de l’or mais l’histoire ne dit pas ce qui advint de lui.

ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

Le principe d’Archimède

Pour l'énoncé «habituel» du principe d'Archimède, cliquez ICI.

Le fameux principe devenu loi ou théorème a en fait été démontré au XVIème siècle. Son énoncé figure dans un des ouvrages d’Archimède: « Le Traité des corps flottants »

Proposition III: Un solide de même volume et de même poids (en fait de même masse volumique) que le liquide dans lequel il est abandonné y enfoncera de façon à n’émerger nullement au-dessus de la surface, mais à ne pas descendre plus bas.

Proposition IV: Tout corps plus léger que le liquide où il est abandonné ne sera pas complètement immergé, mais restera en partie au-dessus de la surface du liquide.

Proposition V: Un solide plus léger que le liquide dans lequel on l’abandonne y enfonce de telle façon qu’un volume de liquide égal à la partie immergée ait le même poids que le solide entier.

Proposition VI: Lorsqu’un corps est plus léger que le liquide où on l’enfonce et remonte à la surface, la force qui pousse en haut ce corps a pour mesure la quantité dont le poids d’un égal volume de liquide surpasse le poids même du corps.

Proposition VII: Un corps plus lourd que le liquide où on l’abandonne descendra au fond et son poids, dans le liquide, diminuera d’une quantité mesurée, par ce que pèse un volume de liquide égal à celui du corps.

Soit en schémas:

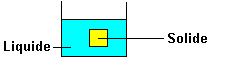
Proposition III

Masse volumique du solide = masse volumique du liquide:
le solide reste en équilibre au sein du liquide où on l’a mis.

Proposition IV

Masse volumique du solide < masse volumique du liquide:
le solide flotte sur le liquide.

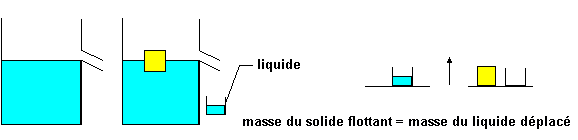
Proposition V

Proposition VI

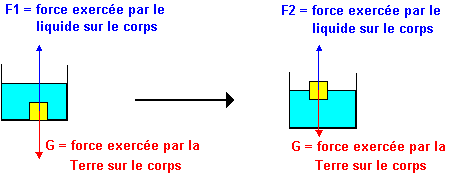F1 > G: le corps remonte	Le volume immergé devient de plus en plus petit: F1 diminue	F1 = G: le corps flotte

Proposition VII

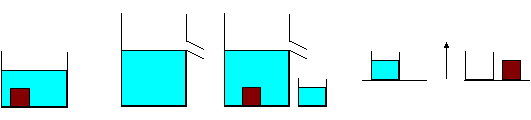Masse volumique du solide > masse volumique du liquide: le solide coule	Masse totale du solide = masse du liquide déplacé

EXPERIENCES, FORMULES et PRINCIPE D'ARCHIMEDE

ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

Autre phrase associée à la légende d’Archimède est le fameux « donnez-moi un levier et je soulèverai le monde». L’ambition du savant était en effet de déplacer des grandes masses à partir de petites.

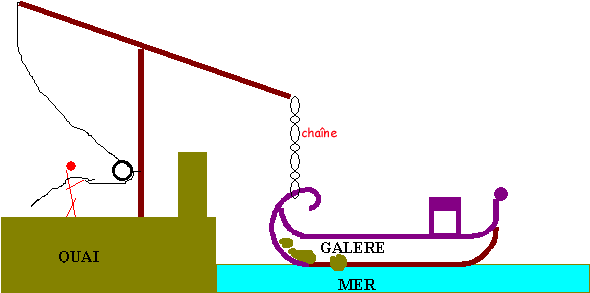
Le déplacement de la galère

Pour prouver au Roi la véracité de son affirmation Archimède lui proposa de déplacer une galère chargée, de plus, sur la terre ferme; ce qui fut dit fut fait. A Syracuse, Archimède, assis, déplaça la galère d’une main en s’aidant sans doute d’un palan.

F = F1 + F2

Cette simple poulie permet de diviser par deux l’effort à effectuer pour tirer l’objet, il faut cependant tirer deux fois plus de corde que la distance du déplacement souhaité et il faut trouver un bon point d’ancrage. En rajoutant des poulies on continue à diviser l’action à exercer.

ANIMATION INTERACTIVE (les systèmes de poulies)

Une autre histoire de galère

Au cours des conflits qui opposèrent Syracuse à Rome, on prêta à Archimède l’invention de nombreuses machines guerrières plus machiavéliques les unes que les autres comme des machines à lancer des flèches et «les mains de fer» qui soulevaient les bateaux et dont le principe basé sur les leviers a été repris au Moyen-Age et à la Renaissance.

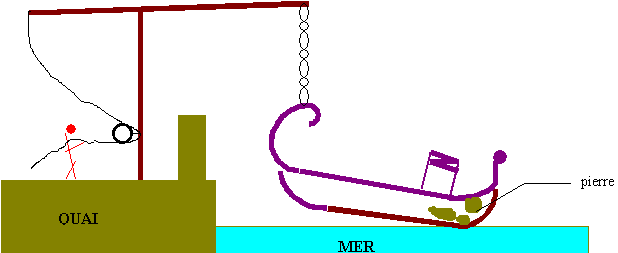
Après avoir été bombardée de pierres, ce qui obligeait l’équipage à refluer vers l’arrière du bateau, la galère était soulevée par un levier associé à une poulie (la force à déployer était donc divisée).

La chaîne était alors détachée et la galère déséquilibrée s’enfonçait.

On trouve dans l’un des ouvrages d’Archimède: «De l’équilibre des plans» la loi des leviers:

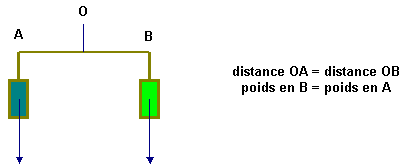
Proposition I: Des poids qui s’équilibrent à des distances égales sont égaux

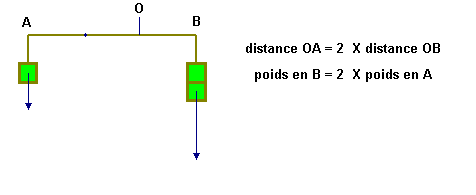
Proposition II: Des poids inégaux s’équilibreront à des distances inégales, et le plus grand sera situé à la plus petite distance.

Proposition III: Des grandeurs quelconques s’équilibrent à des distances inversement proportionnelles à leur poids.

Soit en schémas:

Proposition I

Proposition II et Proposition III

C’est le principe de la balance dite romaine.

ANIMATION INTERACTIVE (la loi du levier)

ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

La plus controversée des légendes d’Archimède est sans doute l’incendie de la flotte romaine par des miroirs. On a tenté de renouveler l’expérience sans succès, et on suppose que cette histoire est plus de «l’intox que de l’info». mais on ne prête qu’aux riches!

Documentation:

• "Les Cahiers de Sciences et Vie"  hors-série du 18 décembre 1993
• Physique et Physiciens par R. Massain - édition Magnard

VOYAGE AU COEUR DE LA GRECE ANTIQUE
(dossier pédagogique par JF Bradu)

ARCHIMEDE | L'HYDROSTATIQUE | LE PRINCIPE D'ARCHIMEDE | LA MECANIQUE | L'OPTIQUE

PRINCIPE D'ARCHIMEDE: expériences, formules et énoncé

RETOUR