Chambre noire (camera obscura) et sténopé: cours d'optique du Prof TNJ

On raconte que l'architecte Della Porta (qui a achevé la coupole de la basilique Saint-Pierre à Rome en 1593) fit l'observation suivante. Il se reposait dans sa chambre à l'heure de la sieste; ayant fermé les volets, la pièce était quasi obscure. Brusquement, en regardant sur le mur opposé à la fenêtre, il cru rêver: il voyait la maison d'en face et les gens marchant dans la rue, bien que tout était à l'envers! Analysant cet étrange phénomène, Della Porta comprit que tout cela était dû à la lumière passant par un tout petit trou dans les volets.

D'autres avaient déjà fait des observations semblables, notamment Léonard de Vinci. à l'époque, on utilisait ce principe pour exécuter rapidement des dessins très fidèles à la réalité. Mais Della Porta comprit que l'on pouvait réaliser des «chambres noires» (camera obscura en italien) en réduction en utilisant une boîte opaque munie d'une petite ouverture (le «sténopé», sténo signifie «serré» en grec) sur une de ses faces et d'une paroi translucide sur la face opposée. Pour obtenir des images plus lumineuses, il remplaça le petit trou par une ouverture plus grande munie d'une lentille. En 1540, Jérôme Cardan pu mettre cette invention au point et la rendre utilisable. Ainsi fut découvert l'ancêtre de la caméra et de l'appareil photographique.

La chambre noire est une boîte opaque dont une face est translucide (verre dépoli, papier calque) et dont la face opposée est percée d'un petit trou appelé sténopé.

L'idéal est d'en fabriquer soi-même et de comparer les observations obtenues pour trouver les paramètres modifiant l'image obtenue.

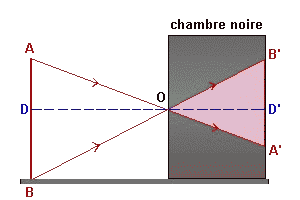Dans un local le plus sombre possible, placer devant l'ouverture de la chambre noire un corps lumineux: flamme d'une bougie, image d'une diapositive projetée sur un mur, ampoule électrique allumée,...

légende du schéma:

AB = taille de l'objet lumineux
O = taille de l'ouverture
A'B' = taille de l'image
DO = distance entre l'objet et l'ouverture
D'O = distance entre l'image et l'ouverture (profondeur de la chambre noire)

Construisez une chambre noire avec laquelle on peut faire varier O et D'O (pas de problème avec DO)

On ne peut faire varier qu'un paramètre à la fois, les autres étant bloqués, pour voir son influence; dans ce cas-ci, on recherche l'influence de paramètres sur les caractéristiques de l'image obtenue.

FACTEURS CONSTANTS:

AB (taille de l'objet lumineux)
luminosité de l'objet lumineux

FACTEURS VARIABLES:

DO (distance entre l'objet et l'ouverture)
D'O (profondeur de la chambre noire)
O (taille de l'ouverture)

CARACTERISTIQUES DE L'IMAGE:

A'B' (taille de l'image)
position (droite = à l'endroit ou renversée = à l'envers)
netteté
luminosité (intensité lumineuse)

	CARACTERISTIQUES DE L'IMAGE
PARAMETRES	A'B'	position	netteté	luminosité
DO augmente	diminue	renversée	augmente	diminue
DO diminue	augmente	renversée	diminue	augmente
D'O augmente	augmente	renversée	discutable!	diminue
D'O diminue	diminue	renversée	discutable!	augmente
O augmente	augmente	renversée	diminue	augmente
O diminue	diminue	renversée	augmente	diminue

La distance entre l'objet et l'ouverture, la profondeur de la chambre noire et la taille de l'ouverture ont de l'influence sur la taille, la netteté et la luminosité de l'image; ces facteurs n'ont pas d'influence sur la position de l'image car elle reste toujours renversée (observations qualitatives).

Pour avoir la meilleur netteté possible, il faut que l'ouverture soit la plus petite possible.

Si l'ouverture est assimillable à un point, alors nous avons les observations quantitatives suivantes:

la taille de l'image est inversément proportionnelle à la distance entre l'objet et l'ouverture;
la taille de l'image est directement proportionnelle à la profondeur de la chambre noire.

La luminosité n'est pas quantifiable objectivement, mais il semblerait qu'elle soit inversément proportionelle à la distance entre l'objet et l'ouverture, et inversément proportionnelle à la profondeur de la chambre noire.

Le modèle ci-contre rend compte des observations.

Les triangles ABO et A'B'O sont semblables (voir cours de géométrie):

donc: AB/A'B' = AO/A'O = BO/B'O = DO/D'O

On peut donc résoudre des problèmes d'optique grâce à la géométrie: c'est le but de l'optique géométrique.