| La réfraction de la
lumière: Première partie: surfaces planes |
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() Introduction: premières observations
Introduction: premières observations
 |
La figure ci-contre montre une observation
courante qu'on ne remarque même plus. La lumière se propage en ligne droite, sauf dans de nombreux cas; ne parlons pas de la lumière qui est déviée lorsqu'elle touche un corps opaque (réflexion, diffusion,...), mais de la lumière se propageant dans des milieux transparents. Analysons le document:
|
| La lumière
venant du crayon, des stores et du fond du verre a été
déviée par l'eau et le verre: lorsque la lumière passe
d'un milieu transparent dans un autre, elle est déviée.
Le crayon semblant «fracturé», ce phénomène est
appelé la réfraction
de la lumière. Dans cette partie, nous étudieront la réfraction dans le cas de surfaces (interfaces) de séparation planes. On parle alors de dioptres plans (dia = à travers, opthesthai = voir, en grec): un dioptre est donc la surface séparant deux milieux transparents différents (l'eau et l'air, par exemple). |
|
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() Observations avec un aquarium contenant de l'eau (les dioptres sont plans)
Observations avec un aquarium contenant de l'eau (les dioptres sont plans)
| Regardez l'aquarium de face:
|
Observations:
|
| A présent, observez cet aquarium sous d'autres angles. | Nous observons bien le phénomène de réfraction de la lumière, mais aussi un phénomène de réflexion totale de celle-ci sans miroirs. La position de l'observateur modifie les caractéristiques des observations. |
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() Etude de la réfraction (cas des dioptres
plans)
Etude de la réfraction (cas des dioptres
plans)
Avec l'aquarium
Utilisation d'un faisceau laser: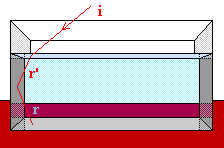 Modifiez l'amplitude de l'angle d'incidence, observez le passage de la lumière de l'eau dans l'air, de l'air dans l'eau puis dans l'air,... Observez donc le visage d'un condisciple en partie derrière l'aquarium. |
Pour visualiser le trajet suivi par la
lumière, nous utilisons le fin faisceau lumineux d'un
laser. Pour rendre le trajet de la lumière visible dans
l'eau, il suffit d'y verser un peu de fluorescéine
(colorant fluorescent) ou quelques gouttes de lait. Il
suffit souvent de s'arranger pour que le faisceau
lumineux "rase" les parois de l'aquarium pour
le visualiser, mais on doit beaucoup tâtonner.
|
|
| L'aquarium est intéressant, mais pas très pratique, surtout si on veut quantifier les observations en mesurant l'amplitude des angles, par exemple. | ||
Avec un demi-cylindre transparent
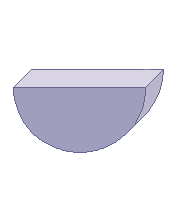 |
Il existe des demi-cylindres comme
représenté ci-contre en verre et en plastique
transparent (polyester); certains sont de véritables
petites boîtes que l'on peut remplir d'eau ou d'autres
liquides transparents. Un demi-cylindre transparent peut être posé sur une feuille de papier. Le trajet du rayon incident, du rayon réfracté et du rayon totalement réfléchi peuvent être repérés (épingles, petits traits au crayon) sur cette feuille: nous avons le schéma en vraie grandeur de diverses manipulations et nous pouvons mesurer l'amplitude des angles avec beaucoup de facilité au moyen d'un rapporteur. Un minimum de soin et de précision sont requis. |
| Observations qualitatives | |||
Dirigeons un fin faisceau lumineux de l'air dans le verre et du verre dans l'air; le faisceau lumineux venant du bas et dirigé vers le centre du demi-cylindre n'est pas dévié car il est normal à la surface du verre, il figure donc la lumière passant du verre dans l'air. |
|||
1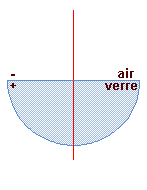 |
2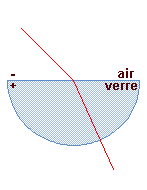 |
3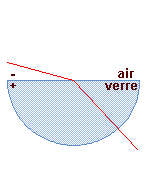 |
4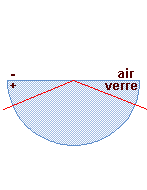 |
| Un rayon normal au dioptre n'est pas dévié. | Un rayon
oblique au dioptre et venant
de l'air se réfracte en se rapprochant
de la normale au point d'incidence. Un rayon oblique au dioptre et venant du verre se réfracte en s'écartant de la normale au point d'incidence. |
Plus l'amplitude de l'angle d'incidence augmente, plus l'amplitude de l'angle de réfraction augmente. Le retour inverse de la lumière: la lumière conserve les mêmes directions qu'elle passe de l'air dans le verre ou du verre dans l'air. |
Lorsque la lumière passe du verre dans l'air, elle ne se réfracte plus vers l'air si l'amplitude de l'angle d'incidence est supérieur à une certaine valeur limite: elle se réfléchit totalement dans le verre. |
| Observations quantitatives | |
Déplacez les rayons avec la souris. Choisissez le "Verre Crown" dont l'indice de réfraction est un rien plus élevé que celui du verre ordinaire; l'indice de réfraction de l'air, dans le cadre de cette expérience, peut être considéré comme égal à celui du vide. (Rappelons que l'incertitude des mesures est de l'ordre du degré) |
Mesurez à présent l'amplitude des angles
d'incidence et celle des angles de réfraction (ou de
réflexion totale) correspondants; faites varier
l'amplitude de l'angle d'incidence de 10° en partant de
0°). Réalisez un tableau pour le passage de la lumière de l'air dans le verre et un autre pour le passage de la lumière du verre dans l'air (vous pouvez combiner les deux en vertu du principe du retour inverse de la lumière, mais je ne le vous conseille pas); distinguez cependant le phénomène de réfraction et celui de réflexion totale. Vos résultats ne seront pas plus précis que ceux calculés dans la figure interractive ci-contre: 1 ou 2 degrés de tolérance. Pour plus de précision, cliquez ici. Vous risquez de ne pas trouver seuls la relation existant entre les valeurs notées. |
| Tableau des mesures | ATTENTION: * = réflexion totale | |||||||||||||||||||||||||||||||||||||||||||||
VIDE
|
VERRE
|
Quel est le rapport entre
l'amplitude de l'amgle d'incidence et l'amplitude de
l'angle de réfraction ? C'est Descartes qui énonça le premier les lois de la réfraction et c'est Snell qui en rédigea la version que nous connaissons actuellement. Si vous avez étudié un peu de trigonométrie, la loi suivante ne vous rebutera pas: sin I ° / sin R' ° = k (une constante) cette constante est appelée "indice de réfraction" du milieu le plus réfringent par rapport au milieu le moins réfringent (le vide ou l'air, généralement) et est noté n (voyez le tableau des indices de réfraction). |
||||||||||||||||||||||||||||||||||||||||||||
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() Lois de la réfraction
Lois de la réfraction
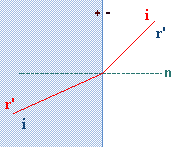 |
Légende: i = rayon incident |
Lois de la réfraction: 1 : Le rayon incident, le rayon réfracté et la normale au point d'incidence appartiennent à un même plan. Ces rayons sont situés de part et d'autre du dioptre. 2 : Tout rayon incident normal au dioptre n'est pas réfracté. 3 : L'amplitude de l'angle d'incidence et celle de l'angle de réfraction (par rapport à la normale au point d'incidence) sont différentes, mais elles varient dans le même sens. Le rapport entre le sinus de l'angle d'incidence et le sinus de l'angle de réfraction est constant (c'est l'indice de réfraction). 4 : Le principe du retour inverse de la lumière: le trajet de la lumière est indépendant du sens de la propagation (pour un trajet donné, la lumière peut se propager dans les deux sens). Rappel:
|
|
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() La réflexion totale
La réflexion totale
Observations
| Manipulez
la figure
interactive ou celle-ci. Lorsque la lumière passe d'un milieu plus réfringent (exemple: l'eau) dans un milieu moins réfringent (exemple: l'air), les rayons réfractés s'écartent de la normale. L'angle limite au-delà duquel le rayon réfracté rase la surface est appelé angle limite de réfraction (l). Si l'amplitude de l'angle d'incidence s'accroît au-delà de celle de l'angle limite de réfraction, la lumière ne quitte plus le milieu (dans ce cas: l'eau), elle se réfléchit sur la surface comme sur un miroir, c'est le phénomène de réflexion totale.
|
Quand y a-t-il réflexion totale ?
Deux
conditions doivent être remplies:
|
Illustration
| Une FIGURE INTERACTIVE peut vous aider à mieux visualiser ce phénomène. |
Applications
| Les fibres optiques (pour une visualisation interactive, cliquez ICI), les prismes à l'intérieur des jumelles et des périscopes, les fontaines lumineuses,... |
INTRODUCTION | OBSERVATIONS | ETUDE DE LA REFRACTION | LOIS DE LA REFRACTION | REFLEXION TOTALE | PLUS
![]() Plus ?
Plus ?
|
RETOUR à la page d'OPTIQUE